Wir suchen den größten und kleinsten Wert einer Funktion
![]()
| (1) | Suche alle Punkte, in denen |
| (2) | Bestimme alle stationären Punkte von |
| Löse |
|
| (3) | Berechne |
| (4) | Größter Wert |
| kleinster Wert |
Es ist nicht notwendig ![]() zu berechnen.
zu berechnen.
BEISPIEL
Gesucht sind die globalen Extrema der Funktion
![]()
| globales Minimum | ||
| globales Maximum |
Die globalen Extremwerte existieren nicht immer und sind auch nicht immer eindeutig bestimmt.
BEISPIEL
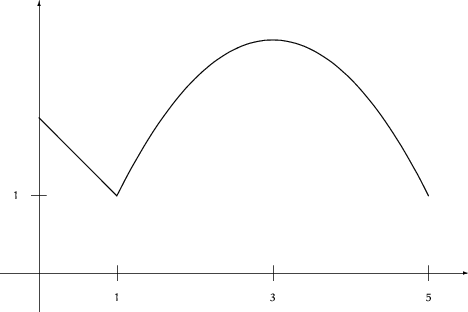
Wir suchen die globalen Extrema der Funktion
![]()
![$x\mapsto
\left\{ \begin{array}
{ll}
\vert x-1\vert+1 & \mbox{für }0\leq x\leq...
...[1ex]
\frac{1}{2}(-x^2+6\,x+3) & \mbox{für }1 < x\leq 5\\ \end{array} \right.$](img1042.gif)
Im Intervall ![]() ist
ist
![]() .
.
Der einzige stationäre Punkt in ![]() (!)
ist daher
(!)
ist daher ![]() .
.
| globales Minimum | ||
| globales Maximum | ||
| globales Minimum |
Das globale Maximum ist ![]() , die globalen Minima sind
, die globalen Minima sind
![]() und
und ![]() .
.
Im Falle eines unbeschränkten (z.B. ![]() ) oder offenen
(z.B.
) oder offenen
(z.B. ![]() ) Definitionsbereichs, berechnen wir anstatt der
Funktionswerte an den Randpunkten
) Definitionsbereichs, berechnen wir anstatt der
Funktionswerte an den Randpunkten ![]() und
und ![]() die entsprechenden
Grenzwerte
(z.B.
die entsprechenden
Grenzwerte
(z.B. ![]() oder
oder
![]() ).
Falls einer dieser Grenzwert größer oder kleiner als jeder
Funktionswert ist, so existiert das Maximum bzw. Minimum nicht.
).
Falls einer dieser Grenzwert größer oder kleiner als jeder
Funktionswert ist, so existiert das Maximum bzw. Minimum nicht.
BEISPIEL
Wir suchen die globalen Extrema der Funktion
![]() .
.
| globales Minimum | ||
| das globale Maximum | ||
| existiert nicht |