Im lokalen Minimum
Im lokalen Minimum ![]() unseres
Beispiels
berührt die Gerade
der Nebenbedingung eine Isoquante.
unseres
Beispiels
berührt die Gerade
der Nebenbedingung eine Isoquante.
Daher müssen in diesem Punkt die Gradienten von ![]() und
und ![]() ,,parallel`` sein (der Gradient steht immer normal auf die
Niveaulinien), d.h.
,,parallel`` sein (der Gradient steht immer normal auf die
Niveaulinien), d.h.
![]()
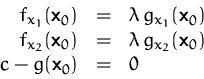
Wir erzeugen uns aus ![]() ,
, ![]() und einer Hilfsvariablen
und einer Hilfsvariablen ![]() eine neue Funktion, die Lagrange-Funktion
eine neue Funktion, die Lagrange-Funktion
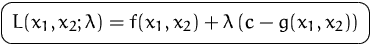
Die Hilfsvariable ![]() heißt Lagrange-Multiplikator.
heißt Lagrange-Multiplikator.
Wenn die Nebenbedingung erfüllt ist, so stimmen ![]() und
und ![]() überein.
Die stationären
Punkte
der Lagrange-Funktion erfüllen gerade obige
Bedingungen, d.h. sie sind die gesuchten stationären Punkte der
Funktion
überein.
Die stationären
Punkte
der Lagrange-Funktion erfüllen gerade obige
Bedingungen, d.h. sie sind die gesuchten stationären Punkte der
Funktion ![]() unter der Nebenbedingung
unter der Nebenbedingung ![]() :
:
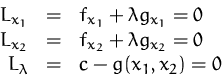
BEISPIEL
Wir suchen die stationären Punkte von
(vgl.)
![]()
![]()
Die Lagrange-Funktion lautet:
![]()
Die stationären Punkte von ![]() erhalten wir durch Nullsetzen der
ersten partiellen Ableitungen:
erhalten wir durch Nullsetzen der
ersten partiellen Ableitungen:
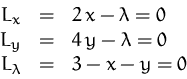
Der einzige stationäre Punkt von ![]() unter der Bedingung
unter der Bedingung ![]() ist somit
ist somit ![]() .
.