| (1) | Wir stellen eine erweiterte Matrix auf, die links die zu invertierende Matrix und rechts die (entsprechend dimensionierte) Einheitsmatrix enthält. |
| (2) | Wir formen die erweiterte Matrix mit den Umformungsschritten des Gaußschen Eliminationsverfahrens so um, daß die linke Seite zur Einheitsmatrix wird. |
| (3) | Entweder ist das Verfahren erfolgreich, dann erhalten wir auf der rechten Seite die inverse Matrix. |
| (4) | Oder die Matrix ist singulär (d.h. sie hat nicht vollen Rang), dann bricht das Verfahren ab. (Wir erhalten auf der linken Seite eine Zeile aus Nullen.) |
BEISPIEL
Wir suchen die inverse Matrix zu
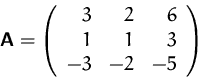
(1) Wir stellen die erweitere Matrix auf:
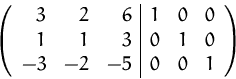
(2) Durch Umformen erhalten wir daraus
![]()
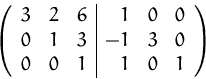
Die ursprüngliche Matrix liegt nun in oberer Dreiecksform vor.
Weiteres Umformen ergibt
![]()
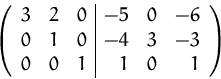
Und schließlich
![]()
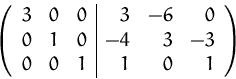
Zuletzt müssen wir noch die Diagonalmatrix in eine Einheitsmatrix umformen.
![]()
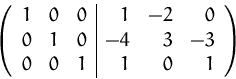
(3) Die Matrix ist daher invertierbar und ihre Inverse ist
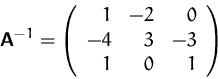
BEISPIEL
Wir suchen die Inverse von
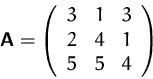
(1) Die erweitere Matrix:
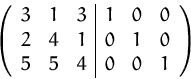
(2) Durch Umformen erhalten wir
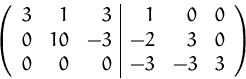
(4) Die Matrix ![]() hat nicht vollen Rang ist daher auch
nicht invertierbar.
hat nicht vollen Rang ist daher auch
nicht invertierbar.